La entrada de hoy es realmente breve. El sueño pronto me va a vencer, por lo que voy a economizar las palabras y dejarles algunas curiosidades matemáticas. La matemática es fascinante, a pesar de que en la escuela se hayan empeñado por dejarnos un mal sabor con su práctica. No es necesario realizar ninguna compleja integral o estudiar un largo teorema para entender la matemática. Basta con jugar con los números y descubrir los secretos que ellos guardan. Jugando con los números es como se ejercita la lógica y de tanto en tanto se descubre alguna ley o propiedad que es útil a otros para aplicar las matemáticas en diferentes campos. Así que ahí vamos con algunas curiosidades:
Números muy grandes
¿Como podemos determinar cual de estos números es el mayor?
A = 2^2^2^55
B = 3^3^3^43
Si tratamos de hacerlo a la fuerza bruta, con la calculadora científica, nos vamos a encontrar con un mensaje de error. El número es demasiado grande como para poder calcularlo de esta forma. Incluso utilizando un software como Matlab nos encontraremos con un paredón. El 2^55 o el 3^43 se pueden calcular, pero luego la cosa se hace cuesta arriba... y ni se nos ocurre tratar de calcularlo con lápiz y papel, necesitaríamos varias vidas para terminar. Bueno, la solución rápida al dilema es emplear las propiedades de los logarítmos:
Ln(Ln(A)) = Ln(Ln(2)) + [Ln(2)*2^55] = 2.4973 x10^16
Ln(Ln(B)) = Ln(Ln(3)) + [Ln(3)*3^43] = 3.6063 x10^20
Esta cuenta si se puede hacer con una calculadora científica normal, y facilmente se puede verificar que B > A.
Los números de Lychrel y el 196
Tomemos un número entero cualquiera y sumemosle su versión invertida. Por ejemplo, el 65
65 + 56 = 121
Bien, el número obtenido es un capicúa, o sea, que se lee igual de izquierda a derecha que de derecha a izquierda. Tomemos otro número, por ejemplo, el 76:
76 + 67 = 143 --> 143 + 341 = 484
Nuevamente, hemos obtenido un capicúa luego de iterar dos veces el proceso. Bueno, hechos los ejemplos, paso a contarles que es un número de Lychrel: es un número natural de base 10 con el que no se obtiene un número capicúa como resultado del proceso iterativo descrito en los ejemplos. En la práctica se ha verificado que con casi cualquier número se termina obteniendo un número capicúa, y lo único que difiere es la cantidad de iteraciones necesarias, que puede ir desde 1 (como en el caso del 65) hasta 55 pasos (para el 10911), y más aún en casos de números de más cifras. Hasta ahora no se ha podido demostrar que exista algún número de Lychrel, pero tampoco se ha podido demostrar que no existan. Existen algunos números que se resisten a entregar un capicúa al ser sometidos al proceso iterativo antes mencionado, y el menor de estos es el 196. En mayo de 2006, el matemático Wade VanLandingham llegó a un número de 300 millones de dígitos, después de 724756966 iteraciones, y el capicúa se negó a aparecer. Por ese motivo se cree que el 196 es el primer número de Lychrel, aunque hasta que no pueda ser demostrado en forma total mediante algún procedimiento matemático la duda seguirá persistiendo.
La espiral de Teodoro o de Einstein
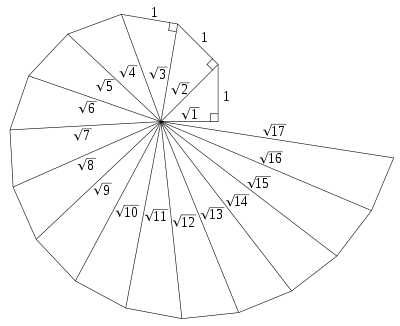
Este es un ejercicio bien gráfico. Tomemos un triángulo rectángulo cuyos catetos son de longitud 1. Como es bien sabido, la hipotenusa será sqrt(2). Luego, si tomamos la hipotenusa y la utilizamos como uno de los catetos de un nuevo triángulo rectángulo, cuyo otro cateto sigue siendo de longitud 1, la hipotenusa de este otro triángulo sera sqrt(3). Si repetimos el proceso, tomando cada nueva hipotenusa como un cateto de un triángulo rectángulo, y tomamos el segundo cateto como de amplitud unitaria, obtendremos sucesivas hipotenusas con las raíces cuadradas de todos los números enteros. Visto gráficamente, queda así:
Tomemos un número entero cualquiera y sumemosle su versión invertida. Por ejemplo, el 65
65 + 56 = 121
Bien, el número obtenido es un capicúa, o sea, que se lee igual de izquierda a derecha que de derecha a izquierda. Tomemos otro número, por ejemplo, el 76:
76 + 67 = 143 --> 143 + 341 = 484
Nuevamente, hemos obtenido un capicúa luego de iterar dos veces el proceso. Bueno, hechos los ejemplos, paso a contarles que es un número de Lychrel: es un número natural de base 10 con el que no se obtiene un número capicúa como resultado del proceso iterativo descrito en los ejemplos. En la práctica se ha verificado que con casi cualquier número se termina obteniendo un número capicúa, y lo único que difiere es la cantidad de iteraciones necesarias, que puede ir desde 1 (como en el caso del 65) hasta 55 pasos (para el 10911), y más aún en casos de números de más cifras. Hasta ahora no se ha podido demostrar que exista algún número de Lychrel, pero tampoco se ha podido demostrar que no existan. Existen algunos números que se resisten a entregar un capicúa al ser sometidos al proceso iterativo antes mencionado, y el menor de estos es el 196. En mayo de 2006, el matemático Wade VanLandingham llegó a un número de 300 millones de dígitos, después de 724756966 iteraciones, y el capicúa se negó a aparecer. Por ese motivo se cree que el 196 es el primer número de Lychrel, aunque hasta que no pueda ser demostrado en forma total mediante algún procedimiento matemático la duda seguirá persistiendo.
La espiral de Teodoro o de Einstein
Este es un ejercicio bien gráfico. Tomemos un triángulo rectángulo cuyos catetos son de longitud 1. Como es bien sabido, la hipotenusa será sqrt(2). Luego, si tomamos la hipotenusa y la utilizamos como uno de los catetos de un nuevo triángulo rectángulo, cuyo otro cateto sigue siendo de longitud 1, la hipotenusa de este otro triángulo sera sqrt(3). Si repetimos el proceso, tomando cada nueva hipotenusa como un cateto de un triángulo rectángulo, y tomamos el segundo cateto como de amplitud unitaria, obtendremos sucesivas hipotenusas con las raíces cuadradas de todos los números enteros. Visto gráficamente, queda así:
Lo curioso de esta espiral, además de que nos permite obtener en forma gráfica los resultados de raíces como sqrt(2) y sqrt(3), que son irracionales, es que la distancia entre dos vueltas de la espiral tiende a π. Siempre π, no importa de que modelo hablemos, en que campo de la física, la ingeniería, la geometría, o lo que sea, siempre aparece π. Como si fuese una de las claves que permite desentrañar los misterios del universo.
Bueno, creo que eso es todo por hoy. Espero que le haya gustado, y ya volveré con la matemática en breve, con algunas de estas curiosidades. Hasta la próxima.
pues, ahora que leo esta novedad -para mi- sobre la espiral, te recomiendo mas aún "pi", la pelicula...
ResponderEliminar