Hoy no voy a justificar nada, simplemente voy a dejarme llevar por mi gusto por las curiosidades matemáticas, y voy a compartir con ustedes un popurrí de cosas que he ido recopilando en largas horas de navegación por la red. Así que menos palabras y más matemáticas:
1) Números perfectos y binariamente armoniosos
Se dice que un número (natural) es perfecto si es igual a la suma de sus divisores propios positivos. Por ejemplo, el 6 es un número perfecto, porque sus divisores propios son 1, 2 y 3; y 6 = 1 + 2 + 3. Los siguientes números perfectos son 28, 496 y 8128.
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064
Los número perfectos no son comunes. De hecho, apenas se conocen 48. No se sabe si son infinitos, o si existe alguno de ellos que sea impar (ambas son cuestiones abiertas al día de hoy). Sin embargo todos ellos comparten una singular simetría cuando son expresados en base 2 (sistema binario).
2) ¿Que hace Pi en el medio de un río?
El libro "El enigma de Fermat", de Simon Singh, es un buen ejemplo de como contar la historia de las matemáticas, y algunos de sus descubrimientos más abstractos, de una forma amena. En sus páginas encontré una curiosa referencia a una de las singulares relaciones donde aparece el número Pi.
3) Buscando números dentro de Pi
A través de Microsiervos llegué a la página three.onefouronefive.net, en donde se muestran los primeros mil millones de dígitos de Pi, con algunas anotaciones de interés como agregado. Sin embargo, lo más curioso es que se puede buscar un número determinado (el año de nacimiento, el número de documento, el código postal, etc.) dentro de este grupo de mil millones de números, y el programa informa sobre la posición en que aparece por primera vez dentro de la infinita cadena de decimales de Pi. Teniendo en cuenta que, como mencioné, los decimales de Pi son infinitos, a la larga van a aparecer representados todas las secuencias numéricas que se nos puedan ocurrir. Así, por ejemplo, la fecha de creación de este blog (24/07/2010) aparece por primera vez en la posición 273.118.449, la población total de la Argentina según el censo 2010 (40.117.096) aparece en la posición 25.856.456, y la carga eléctrica del protón (160217 yC, la "y" es del prefijo "yocto", 10-24) aparece en la posición 279.290. El propio Pi (tomado como 3,14159) aparece en el 176.451 lugar.
4) El problema de 123456789=100
No lo tomen literalmente, está claro que esa igualdad no es posible. A lo que me refiero es a las diferentes formas en las que se pueden combinar los dígitos del 1 al 9, en orden ascendente, y las operaciones matemáticas (suma, resta, multiplicación, etc.) de forma tal de obtener el número 100. Algunos ejemplos son:
123 - 45 - 67 + 89 = 100.
123 + 4 - 5 + 67 - 89 = 100.
123 - 4 - 5 - 6 - 7 + 8 - 9 = 100.
1 + 23 - 4 + 5 + 6 + 78 - 9 = 100.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8*9 = 100
1 + 23 - 4 + 56/7 + 8*9 = 100
... y así podemos seguir un rato más. Les recomiendo sigan el hilo de comentarios que se armó sobre este tema en el blog matemático Gaussianos.
5) Malabares numéricos
En Futility Closet encontré este, podríamos decir, algoritmo, para jugar con los números. Fue propuesto por R.V. Heath en 1950, y dice así:
- Piense dos números enteros positivos.
- Sumelos y obtenga un tercer número.
- Sume el segundo y el tercer número para obtener un cuarto número.
- Repita la operación hasta obtener diez números.
- La suma de los diez números es once veces el séptimo.
Simple, ¿no es cierto?... y funciona. Se puede demostrar fácilmente con un poco de álgebra:
6) Pi... ¿es siempre 3,14159...?
Uno tiende a pensar que siempre es así, pero en realidad esto solo es cierto si hablamos de geometría euclídea. ¿Qué es la geometría euclídea? Pues la que se basa en los cinco postulados de Euclídes:
Por dos puntos distintos sólo se puede trazar una línea recta.
Todo segmento rectilíneo se puede prolongar indefinidamente.
Con un centro y un radio sólo se puede trazar una circunferencia.
Todos los ángulos rectos son iguales.
Por un punto exterior a una recta se puede trazar una única paralela a la recta dada.
Sin embargo, si el quinto postulado no se cumple, pues entonces estamos hablando de otro tipo de geometría:
Por un punto exterior a una recta no pasa ninguna paralela a la recta dada (geometría elíptica).
Por un punto exterior a una recta pasan infinitas paralelas a la recta dada (geometría hiperbólica).
Trabajar con geometría hiperbólica nos lleva a cosas como que Pi puede tomar cualquier valor por encima de 3,14159; mientras que la geometría elíptica aplicada a una esfera nos da que Pi puede tomar cualquier valor entre -0.6824595 y 3,14159. En fin, es bueno aclarar lo de la geometría euclidiana, porque no vaya a ser que Pi se haga cero, negativo... o infinito.
7) El increíble 1089
El número 1089 tiene algunas características muy especiales. Por ejemplo, si tomamos cualquier número de 3 cifras, por ejemplo el 976, lo damos vuelta (679), se lo restamos al número original (976-679=297), lo damos vuelta (792) y se lo sumamos al resultado (297+792), siempre obtendremos el número 1089.
Como si eso no fuera poco, podemos multiplicar a 1089 por 9 y... 1089 x 9 = 9801, lo hemos dado vuelta.
Pero quizás lo más interesante es que tomando el número 9801, resultado de multiplicar 1089 x 9, y haciendo la inversa (1/9801), se obtiene el siguiente número, 0,0001020304050607…969799, es decir, un número decimal con todos los números enteros del 0 al 99 en su parte decimal, ¡colocados correlativamente!. Bueno todos no, todos, excepto el 98, que aparece al principio del número 9801.
1) Números perfectos y binariamente armoniosos
Se dice que un número (natural) es perfecto si es igual a la suma de sus divisores propios positivos. Por ejemplo, el 6 es un número perfecto, porque sus divisores propios son 1, 2 y 3; y 6 = 1 + 2 + 3. Los siguientes números perfectos son 28, 496 y 8128.
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064
Los número perfectos no son comunes. De hecho, apenas se conocen 48. No se sabe si son infinitos, o si existe alguno de ellos que sea impar (ambas son cuestiones abiertas al día de hoy). Sin embargo todos ellos comparten una singular simetría cuando son expresados en base 2 (sistema binario).
 |
| La increíble simetría de los números perfectos cuando se representan en base 2 [Fuente: Futility Closet]. Para el que quiera probar con números más grandes, les recomiendo visitar la página del MIT, donde están todos los números perfectos, y hacer los cambios de base 10 a 2 en el conversor online WIMS. |
2) ¿Que hace Pi en el medio de un río?
El libro "El enigma de Fermat", de Simon Singh, es un buen ejemplo de como contar la historia de las matemáticas, y algunos de sus descubrimientos más abstractos, de una forma amena. En sus páginas encontré una curiosa referencia a una de las singulares relaciones donde aparece el número Pi.
"Pitágoras descubrió por primera vez la base matemática que rige un fenómeno físico y demostró que se da una relación fundamental entre las matemáticas y la ciencia. Desde entonces, los científicos han buscado los principios matemáticos que, al parecer, gobiernan cada proceso físico elemental y han averiguado que los números afloran en todo tipo de fenómenos naturales. Por ejemplo, un número particular parece presidir las longitudes de los ríos con meandros. El catedrático Hans-Henrik Stolum, geólogo de la Universidad de Cambridge, ha calculado la relación entre la longitud real de los ríos, desde el nacimiento hasta la desembocadura, y su longitud medida en línea recta. Aunque la proporción varía de un río a otro, el valor promedio es algo mayor que 3, o sea, que la longitud real es unas tres veces la distancia en línea recta. En realidad, la relación es aproximadamente 3.14, una cifra muy cercana al valor del número p, la proporción que existe entre la circunferencia de un círculo y su diámetro.
El número pi derivó en su origen de la geometría del círculo y surge una y otra vez en las circunstancias científicas más diversas. En el caso de la relación fluvial, la aparición de p es el resultado de una pugna entre el orden y el caos. Einstein fue el primero en apuntar que los ríos tienden a serpentear cada vez más porque, por leve que sea la curva en un principio, ésta provoca corrientes más veloces en la orilla externa, que van originando una margen más erosionada y cerrada. Cuanto mayor sea la curvatura en la orilla, mayor resulta la velocidad de las corrientes en la margen exterior y, con ella, el aumento de la erosión por ese lado. Así, el curso del río se retuerce cada vez más. Sin embargo existe un proceso natural que detiene el caos: el aumento del serpenteo acaba haciendo que el curso se repliegue sobre sí mismo y se «cortocircuite». El río vuelve a enderezarse y el meandro queda abandonado a un lado, convertido en un lago en forma de herradura. El equilibrio entre estos dos factores opuestos conduce a una relación promedio de p entre la longitud real y la distancia en línea recta desde el nacimiento hasta la desembocadura. La proporción de p aparece con mayor frecuencia en ríos que fluyen por llanuras de pendientes muy suaves, como las que hay en Brasil o en la tundra de Siberia."
 |
| La relación entre la longitud lineal y la longitud real de los ríos puede entenderse mejor analizando los meandros como porciones de circunferencias [Fuente: The river whisperer]. |
3) Buscando números dentro de Pi
A través de Microsiervos llegué a la página three.onefouronefive.net, en donde se muestran los primeros mil millones de dígitos de Pi, con algunas anotaciones de interés como agregado. Sin embargo, lo más curioso es que se puede buscar un número determinado (el año de nacimiento, el número de documento, el código postal, etc.) dentro de este grupo de mil millones de números, y el programa informa sobre la posición en que aparece por primera vez dentro de la infinita cadena de decimales de Pi. Teniendo en cuenta que, como mencioné, los decimales de Pi son infinitos, a la larga van a aparecer representados todas las secuencias numéricas que se nos puedan ocurrir. Así, por ejemplo, la fecha de creación de este blog (24/07/2010) aparece por primera vez en la posición 273.118.449, la población total de la Argentina según el censo 2010 (40.117.096) aparece en la posición 25.856.456, y la carga eléctrica del protón (160217 yC, la "y" es del prefijo "yocto", 10-24) aparece en la posición 279.290. El propio Pi (tomado como 3,14159) aparece en el 176.451 lugar.
4) El problema de 123456789=100
No lo tomen literalmente, está claro que esa igualdad no es posible. A lo que me refiero es a las diferentes formas en las que se pueden combinar los dígitos del 1 al 9, en orden ascendente, y las operaciones matemáticas (suma, resta, multiplicación, etc.) de forma tal de obtener el número 100. Algunos ejemplos son:
123 - 45 - 67 + 89 = 100.
123 + 4 - 5 + 67 - 89 = 100.
123 - 4 - 5 - 6 - 7 + 8 - 9 = 100.
1 + 23 - 4 + 5 + 6 + 78 - 9 = 100.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8*9 = 100
1 + 23 - 4 + 56/7 + 8*9 = 100
... y así podemos seguir un rato más. Les recomiendo sigan el hilo de comentarios que se armó sobre este tema en el blog matemático Gaussianos.
5) Malabares numéricos
En Futility Closet encontré este, podríamos decir, algoritmo, para jugar con los números. Fue propuesto por R.V. Heath en 1950, y dice así:
- Piense dos números enteros positivos.
- Sumelos y obtenga un tercer número.
- Sume el segundo y el tercer número para obtener un cuarto número.
- Repita la operación hasta obtener diez números.
- La suma de los diez números es once veces el séptimo.
Simple, ¿no es cierto?... y funciona. Se puede demostrar fácilmente con un poco de álgebra:
6) Pi... ¿es siempre 3,14159...?
Uno tiende a pensar que siempre es así, pero en realidad esto solo es cierto si hablamos de geometría euclídea. ¿Qué es la geometría euclídea? Pues la que se basa en los cinco postulados de Euclídes:
Por dos puntos distintos sólo se puede trazar una línea recta.
Todo segmento rectilíneo se puede prolongar indefinidamente.
Con un centro y un radio sólo se puede trazar una circunferencia.
Todos los ángulos rectos son iguales.
Por un punto exterior a una recta se puede trazar una única paralela a la recta dada.
Sin embargo, si el quinto postulado no se cumple, pues entonces estamos hablando de otro tipo de geometría:
Por un punto exterior a una recta no pasa ninguna paralela a la recta dada (geometría elíptica).
Por un punto exterior a una recta pasan infinitas paralelas a la recta dada (geometría hiperbólica).
Trabajar con geometría hiperbólica nos lleva a cosas como que Pi puede tomar cualquier valor por encima de 3,14159; mientras que la geometría elíptica aplicada a una esfera nos da que Pi puede tomar cualquier valor entre -0.6824595 y 3,14159. En fin, es bueno aclarar lo de la geometría euclidiana, porque no vaya a ser que Pi se haga cero, negativo... o infinito.
 |
| Si trabajamos con geometría hiperbólica, Pi puede tomar cualquier valor real por encima de 3,14159. |
7) El increíble 1089
El número 1089 tiene algunas características muy especiales. Por ejemplo, si tomamos cualquier número de 3 cifras, por ejemplo el 976, lo damos vuelta (679), se lo restamos al número original (976-679=297), lo damos vuelta (792) y se lo sumamos al resultado (297+792), siempre obtendremos el número 1089.
Como si eso no fuera poco, podemos multiplicar a 1089 por 9 y... 1089 x 9 = 9801, lo hemos dado vuelta.
Pero quizás lo más interesante es que tomando el número 9801, resultado de multiplicar 1089 x 9, y haciendo la inversa (1/9801), se obtiene el siguiente número, 0,0001020304050607…969799, es decir, un número decimal con todos los números enteros del 0 al 99 en su parte decimal, ¡colocados correlativamente!. Bueno todos no, todos, excepto el 98, que aparece al principio del número 9801.
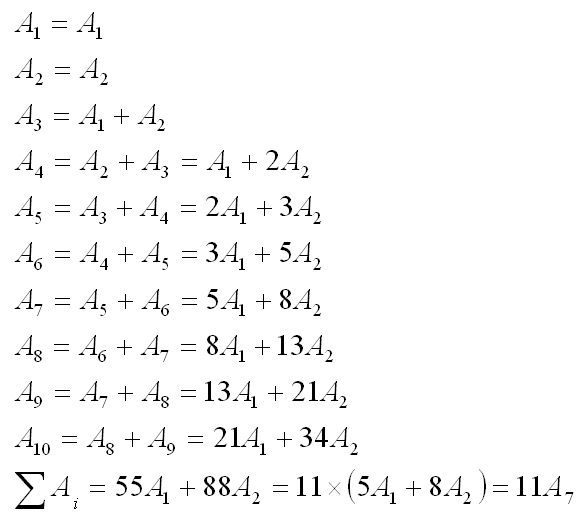

De los numeros perfectos, de su simetria binaria, podria intuirse al menos que no hay numeros perfectos impares.
ResponderEliminarTodos los numeros binarios terminados en 0 dan como resultado un numero par.
El 3er ¨axioma¨ resulta interasante que a nadie se le halla ocurrido como sistema de encriptación.
Es decir, si todo numero aparece indefectiblemente dentro de los decimales de Pi, podria utilizarse para enviar un numero encriptado, la coordenada de dicho numero ¿no?
Buena observación Alejandro. Lo que queda por demostrar es que todos los números perfectos son simétricamente binarios. Hasta ahora parece que sí, pero hasta que no haya una demostración algebraica cerrada no deja de ser una conjetura. En cuanto a lo de usar a PI como sistema de encriptación, pues no es mala idea. De hecho, podríamos usar números irracionales típicos, como e, sqrt(2), sqrt(3), etc., que también tienen infinitos decimales no períodicos. Abrazo
Eliminar